기술자료
motorland
05. 자기이력곡선
자기이력곡선의 해석
자성체를 그림 1]과 같이 코일 안에 넣고 코일에 전류가 어느 정도 세기 이상으로 흐르면 무질서하게 흩어져 있던 자성체 내의 원자자석들의 N극과 S극이 일정한 방향으로 정렬되어 착자됩니다.
반대로 원자자석들의 극성을 무질서하게 흐트러뜨려 자성체의 외부로 자력선이 방출되지 못하게 되는 것을 탈자라고 합니다. 여기서 우리는 자성체를 착탈자 시키는 과정을 되풀 이하며 곡선을 그려보면 자성재료의 특성을 알 수 있습니다. 이러한 곡선을 자기이력곡선(회 ) 일명, Hysterisis curve라고도 하는데 자성재료마다 제각각 특유한 곡선으로 나타나기 때문에 이 곡선을 해석하면 잔류자속밀도(Br)나 보자력(bHc, iHc) 또는 최대 에너지적(BH max)과 리코일투자율 등을 알 수 있어 이 곡선의 물리적 해석을 이해하는 것은 DC모터를 연구하고 개발하는데 매우 중요합니다. 코일에 흐르는 전류에서 방출되는 자력선에 의한 자계 H와 이 자계에 의하여 착자된 자석에서 나오는 자력선에 의한 자계와의 관계를 그래프로 그린 곡선을 말합니다.
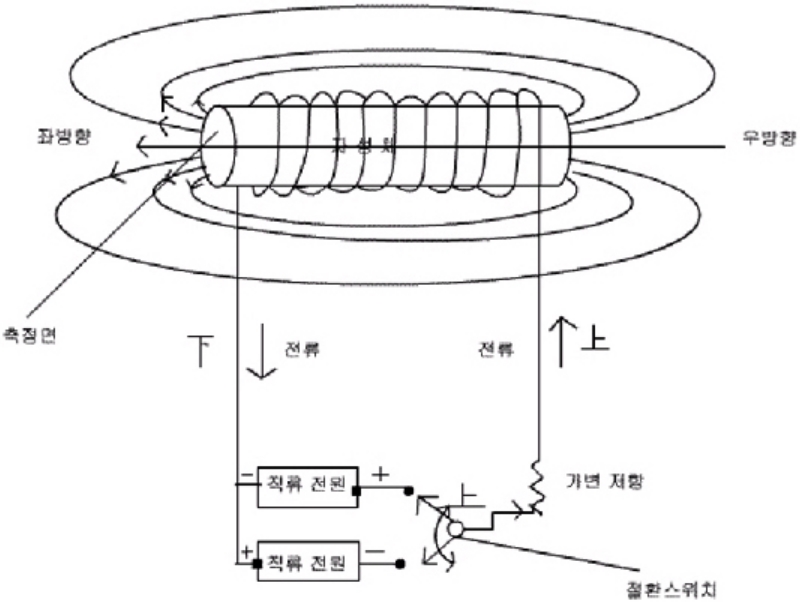 그림1. 전류와 자력선의 방향
그림1. 전류와 자력선의 방향
여기서 B-H곡선과 4 Ti곡선의 물리적인 설명해 보겠습니다. 만약 여러분이 이 두 곡선의 의미를 충분히 이해하지 못했다면 그 이상 자석의 특성을 이해하고 자석을 이용해 무엇인가를 설계하기가 쉽지 않으므로 이 두 곡선의 의미를 충분히 이해하는 것이 매우 중요합니다. [그림1]과 같이 코일 내부에 자성체 (자성체와 자석의 차이점은 자석은 자성체의 원자자석을 정렬시켜 외부로 자력선이 나오도록 착자가 완료된 소재를 말하는데 반해 자성체란 자석이 될 수 있는 모든 소재를 일컫는 말입니다. 따라서 흔히 자성체하면 착자되지 않은 소재 를 의미합니다.)를 넣고 측정면에서 자력을 측정하면서 곡선을 그려봅니다.
먼저 절환 스위치를 위(上)로 한 후 가변저항을 무한대로 크게 하면 전류가 흐르지 않아 코일에서 나오는 자력선이 없으며 자성체도 착자되지 않은 상태 이므로 측정면에서의 자력선도 없어 [그림2]에서 NG도 S극도 아닌 0점이 됩니다.
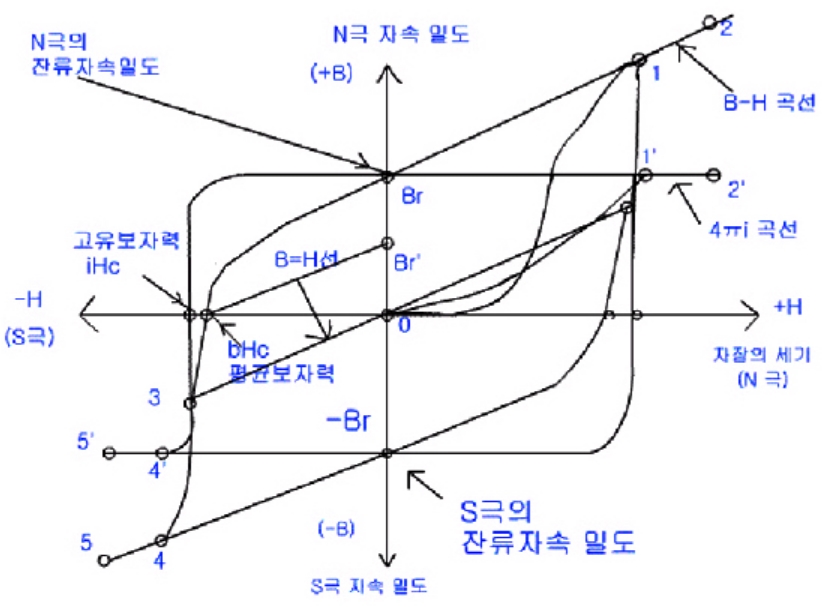 그림2. 자기이력 곡선
그림2. 자기이력 곡선
가변저항을 서서히 줄여나가면 코일의 전류는 방향으로 흐르기 시작하는데 코일의 내부에서 방향으로 N극의 자력선이 나오게 되며 코일 안의 자성체도 전류를 점점 세게 흘리는 것에 비례하여 더 많은 원자자석들이 정렬되면서 점점 착자가 강하게 진행되어 좌측은 N극, 우측은 S극으로 착자됩니다 어느 정도 이상의 전류치가 되면 모든 원자자석들이 완벽하게 한 방향으로 정렬된 상태인 포화착자(Full magnetization) 상태가 되며, 이때까지의 곡선은 [그림2]와 같이 0점으로부터 점차로 변화되어 측정면에서 N극을 띠게 되며 1상한 면에서 포화점 1 및 1'로 됩니다.
다시 전류를 더 세게 보내면 코일(Coil)에서는 더 큰 자력선이 방출되어 점2로 되면서 자력의 세기가(N극) 더욱 세게 측정되지만 자석 자체는 착자가 이미 포화된 상태(포화 착자)이므로 그 소재가 낼 수 있는 최대의 자력선을 외부로 방출하는 자력선은 더 이상 늘 수 없게 되어 전류가 커지더라도 자석만이 방출하는 자력선의 크기는 점1' = 2' 로서 동일하게 됩니다. 이 과정을 그림 4] 에서 보면 자석과 외부자계의 자력선이 함께 이루어져 나타나는 B-H곡선의 경우는 전류가 0에서 점점 커짐에 따라 [0 -1 → 2]와 같이 되어 이론상으로는 그 이상 무한히 커질 수 있습니다.
그러나 자석 자체의 곡선인 4pi곡선은 전류가 0에서 점점 커짐에 따라 [0 -1 2]와 같이 되어 1점을 넘어서면 코일에 아무리 큰 전류를 흘려 보내더라고 착자된 자석의 N극의 세기는 더 이상 커지지 않게 되는데 이 점1' 를 포화착자점이라고 부릅니다.
여기서 거꾸로 가변저항을 무한대로 크게 하여 코일에 흐르는 전류를 0으로 없애면 B-H곡선은 코일에서 나오는 자력선 즉, 외부자계 H가 0이 되기 때문에 자석(자성체)에 남아 있는 잔류자속 만큼만 측정면에서 읽혀지게 되고 그 크기가 Br의 크기인 것입니다.(2 - 1 - Br) 여기서 Br을 잔류자속밀도라고 합니다. 물론 자석자체의 자력선 방출곡선인 4 T i곡선도 비록 코일에서 전류는 흐르지 않지만 자연상태에서 감자나 탈자가 일어나지 않은 상태이므로 잔류자속 Br점으로 돌아오게 됩니다.(214 1 - br) 즉, 한번 포화 착자시킨 자석은 비록 그 자석을 착자시킨 코일의 자력선 (외부자계 H)이 전류가 0이 되어 없어 졌다고 해도 자석 자체에는 원자자석들이 이미 정렬 되어 자력선이 외부로 방출되는 상태가 되었으므로 자력을 띠게 되는 것입니다. 이와 같이 자석을 포화 착자시켰다가 외부자계를 제거시킨 상태에서 자석 자체에 남아 있는 자속을 우리는 잔류지속밀도(Br=B residual)라고 부릅니다.
이제는 지금과는 정반대로 그림1]의 절환스위치를 F방향으로 놓고 가변저항을 다시 서서히 줄여가며 코일에 전류가 흐르기 시작함녀 코일은 우방향으로 N극, 좌방향으로는 S극이 되면서 서서히 많은 자력선을 방출하게 됩니다.
따라서 측정면에서의 자속량 변화는 자석의 N극의 세기와 코일의 S극의 세기가 반대 방향이므로 각각 상쇄되어 B-H곡선(B자석에서 나오는 자력선의 세기에서 H코일에서 나오는 자력선 즉, 외부자계의 세기를 뺀 자력의 세기를 나타내는 곡선을 말하며 문자 그대로 B minus H 곡선이라고 부릅니다.)은 2상한에서와 같이 점점 N극의 세기가 줄어들게 되지만 자석자체의 자속량은 어느 정도의 외부자계에 대항하면서 N극의 세기를 유지하다가 전류치 즉, 외부자계의 세기가 bHc부근을 지나가면서 급격히 감자되기 시작하여 iHc점 즉 B-H곡 선과 BH직선이 서로 만나는 점에 오면 완전히 탈자(무수히 많은 원자자석의 정렬이 흐트러져 자성체 내부에서 원자자석들끼리 자력선을 주고 받는 상태가 되면 더 이상 자성체의 밖으로는 자력선들이 방출되지 않게 되는데 이러한 상태를 탈자된 상태라고 합니다.)되어 버리는 것입니다.
여기서 bhc점의 물리적 의미는 자석의 N극(방향)과 코일의 S극(- 방향 )이 측정면에서 서로 평형을 유지하는 점이며 이점에서는 자석이 상당히 감자 되었지만 아직 완전히 탈자되지 않은 관계로 전류를 끊여도 bHc점에서 Recoil투자율과 평행하게 돌아가 잔류자속이 Br로 줄어들게 됩니다.
또한 iHc(고유보자력 Intrinsic Coercive force 라고 합니다. 자석을 완전히 탈자시키는데 필요한 외부자계의 세기를 의미합니다.)의 물리적 의미는 자석을 완전히 탈자시키는데 필요한 외부자계의 세기를 의미하며 따라서 정확하게 iHc점까지 코일에 전류를 흘려 외부 자계를 자석에 가했다가 전류를 끊어버리면 자석은 완전히 탈자됩니다. 코일에 흐르는 외부자계의 세기가 iHc보다 조금만 커지더라도 자석은 보유극성이 반대로 바뀌어져 착자되기 사작하여 지금 까지의 N극은 S극으로 S극은 N극으로 극성자체가 완전히 바뀌어 버립니다.
코일에 전류를 더욱 세게 보내면 코일에 의한 외부자계는 전류가 커짐에 따라 점점 S극의 자속량이 커지지만 자석은 점 3'에서 S극으로 포화착자 되어 버리기 때문에 더 이상 자속량이 증가되지 않습니다.
곡선 B-H가 BH 직선과 만나는 점 30 iHc가 되며 4 i곡선은 전류에 의한 반대방향의 외부자계가 작용해도 Br점에서 bHc점 부근까지는 잘 감자되지 않고 견디지만 bHc점보다 큰 코일의 외부자계에서는 급격히 감자되면서 점 3iHc)에 이르러서는 N극도 극도 아닌 상태로 완전히 탈자되어 버리는 것입니다. 계속 전류를 크게 하면 측정면에서 N극이 탈자 되어 자성을 잃어버렸던 것이 정반대의 S극으로 착자 되기 시작하여 코일의 외부자계는 점 4를 지나 점 5와 같이 무한히 커지지만 이때 자석자체의 자속량은 4 mi곡선과 같이 포화점 4 = 점 5'로서 S극의 세기가 더 이상 커지지 않게 됩니다.
다시 가변저항을 점점 크게 하여 전류를 차단하면 외부자계 H는 0이 되고 측정면에서는 자석 S극의 잔류자속량 만큼만 측정되어 이점이 -Br로 S극의 잔류자속밀도가 되는 것입니다.
2상한 - 3상한과 4상한 - 1 상한이 서로 대칭이기 때문에 2 . 3상한 곡선만 있으면 자석의 특성을 해석할 수 있게 됩니다.
표1) 자석에서 사용되는 주요 물리특성
| 양 | 기호 | 단위 | SI단위계에서 CGS 단위계로 |
CGS 단위계에서 SI 단위계로 |
|||
|---|---|---|---|---|---|---|---|
| SI 단위계의 경우 | CGS 단위계의 경우 | ||||||
| 명칭(관계식) | 기호 | 명칭(관계식) | 기호 | ||||
| 자속 | Φ | Weber(Φ=BA) | Wb | 맥스웰(ΦBA) | Maxwell | 1Wb=108Maxwell | 1Maxwell=10-9Wb |
| 자속밀도 | B | Tesla | T | Gauss | G | 1T=104 G | 1G=10-4 T |
| 자기유도 | |||||||
| 자기정수(진공투자율) | μo | 미터 당 Henry | H/m | (μo=1) | - | - | - |
| 자계의 강도 | H | 미터 당 암페어 | A/m | Oersted | Oe | 1A/m=4πX10-3Oe 1.25664X10-2Oe |
10e=10/(4π)A/m =79.5775A/m |
| 자계의 강도에 대응하는 공간의 자속밀도 |
μoH | Tesla(μoH) | T | Oersted | Oe | 1T=104 Oe | 10e=10-4 T |
| 자화 | M | 미터당 암페어(M=JμoM) | A/m | Gauss(M=4πJ) | G | 1A/m=10-3G | 1G=103A/m |
| 자기분극 | J | Tesla(J-μoM) | T | Gauss(M=M/4π) | G | 1T=104 /(4π)G | 1G=4πX10-4 T |
| 투자율(절대투자율) | μ | 미터 당 Henry | H/m | - | - | 1H/m107/(4π)=7.95775X105 | 1=4πX10-7H/m =1.25664X10-9H/m |
| 비투자율 (퍼미언스 계수) |
μs | (μs=μ/μo) | - | (μr=μ) | - | ||
| 기자력 | Fm | 암페어(Fm=HL) (UM=H△L) |
A | Gilbert(Fm=HL) (Um=H△L) |
Gilbert | 1A=4πX10-1Gilbert =1.25664Gilbert |
1Gilbert=10/(4π)A =0.795775A |
| 자위차 | Um | ||||||
| 퍼미언스 | A | Henry(Λ=Φ/Fm) | H | Gilbert 당 Maxwell(Λ=Φ/Fm) | Maxwell Gillbert |
1H=109(4π)=7.95775X107 Maxwell/Gillbert |
1Maxwell/Gillbert =4πX10-9H =1.25664X10-9H |
| 자기저항 | Rm | Henry 역수(Rm=Fm/Φ) | H-1 | Maxwell 당 Gillbert (Rm=Fm/Φ) |
Gillbert Maxwell |
1H-1=4πX10-9 =1.25664X10-8 Gilbert/Maxwell |
1Gilbert Maxwell =109/(4π)H-1 =7.95775X107H-1 |
| 자기에너지적 | 체적당 주울(BH) | J/m3 | (BH) | Goe erg/cm3 |
1J/m3=4πX10GOe =1.25664X102GOe =10erg/cm3 |
1Goe-1/(4π)10-1 =7.95775X10-3J/m3 =7.95775X10-2erg/cm3 |
|
| 자기에너지 | E | 주울(BH · AL/2) | J | (BH · AL8π) | erg | 1J=107 erg | 1erg=10-7 J |
| 자기흠인력 | F | 뉴턴 B2A/2μo | N | (B2A/Bπ) | dyn | 1N=105dyn (1N=0.101972kgf) |
1dyn=10-5N (1kgf=9.80655N) |
※ 자료출처
자료출처 1. 자석과 모터 핸드북 저자 : 김준규 발행 (도서출판 한진)
2. 자석이야기 www.mastopia.co.kr

