기술자료
motorland
02. DC motor와 BLDC motor 구동원리
(1) 구조와 구동원리
Motor의 구동은 식 2.1.1과 같은 움직이는 전하가 자기장(자계)내에 있을 때 받는 힘(로렌츠의 힘의 법칙: Lorentz force law)으로 설명된다.
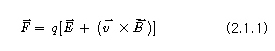
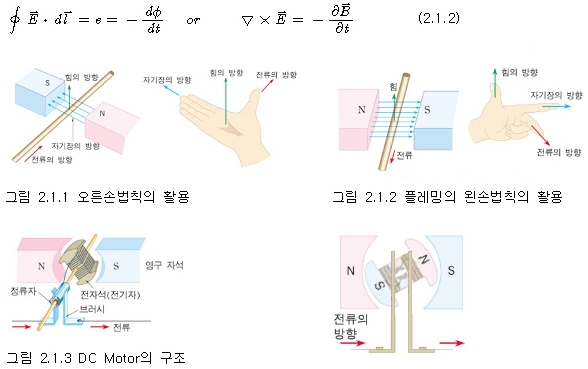
이 로렌트의 힘의 법칙은 유도된 것이 아니라 실험적으로 알게된 하나의 공리이다. 이 법칙은 일반적으로 그림 2.1.1과 그림 2.1.2와 같이 오른손의 법칙 또는 플레밍의 왼손법칙으로 그 방향성을 쉽게 알 수 있도록 알려져 있다. 이 원리를 이용하여 그림 2.1.3과 같이 DC Motor를 만들면 Loop 형태로 이루어진 권선은 자속이 Rotor의 각에 따라 역기전력이 발생하게 되는데 이것은 식 2.1.2와 같은 페러데이의 (전자기 유도) 법칙(Faraday's law)으로 알려져 있다. 즉, 자속(자계)의 시간적인 변화는 기전력(전계)를 형성한다는 것은 알 수 있다.
[주1 - 실제 DC Motor에서의 역기전력은 전자기 유도 법칙에 의한 기전력이 아니라 운동기전력(Motional EMF)이다. 하지만 고정자계 내에서 움직이는 도선에서 발생하는 기전력(운동기전력 : e = tf.dl = Bio )은 상대적으로 고정도선이 시간에 따라 변하는 자계에 놓인 경우(전자기유도 현상) 와 개념적으로 같다. BLDC Motor가 이러한 역의 경우에 해당한다.
이와 같은 구조의 DC Motor를 전기적인 등가회로로 나타내면 그림 2.1.5와 같다. 이러한 등가회로의 전기적인 등가방정식은 식 2.1.3이 된다. (자기회로 저항(RL)은 R에 비하여 매우 크므로 무시)

길이 인 1개의 권선이 자계(자속밀도; 단위면적당 자속) B에서 속도로 움직일 때 역기전력은 식 2.1.2 에서
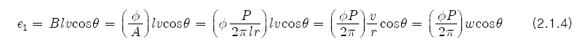
이므로(θ : B와 권선면의 각) 슬롯이 조밀하게 구성되어 있다고 하면 총 연기전력은

와 같다. 반면 토크(T₁)는 식 2.1.1과 식 2.1.4의 계산과정을 이용하면
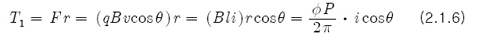
이므로 총 토크는
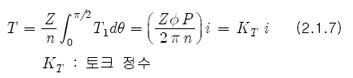
이다. 따라서, 등가방정식 식 2.1.3은
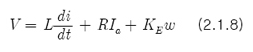
와 같음을 알 수 있고, 정상상태(di/dt=0; i-la)를 고려하고 식 2.1.7을 대입하면
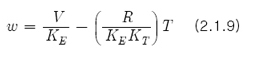
이 되어, 회전속도는 토크와 직선적인 관계가 됨을 알 수 있다. 또한 가동토크(w=0)는
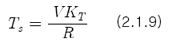
이 된다.
BLDC Motor는 구조적으로 DC Motor와 역의 관계로 설계되어 있으며 그 구동 원리는 근본적으로 같다. DC Motor와 BLDC Motor의 구조를 비교하여 보면 다음과 같다.
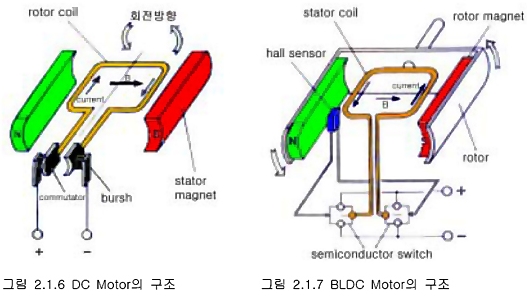
여기서 DC Motor의 정류자(commutator)와 bursh의 역할을 반도체 스위치와 Hall 센서가 하고 있음을 알 수 있다. 또한 DC Motor에서는 고정자계 에서 권선이 회전하면서 운동기전력에 의한 역기전력이 발생함을 알 수 있고, BLDC Motor는 회전자계에서 고정된 권선이 전자기 유도에 의한 역기전 력이 발생함을 알 수 있다.(주석 1. 참조)
BLDC Motor는 동기모터의 한 종류이다. 이것은 고정자(Stator)에 의하여 생성된 자계(Magnetic Field)와 회전자(Rotor)에 의하여 생성된 자계가 같 은 주파수로 회전함을 의미한다. 그리고 Induction Motor에서 발생하는 'slip"발생하지 않는다. BLDC Motor는 single phase, 2-phase, 3-phase 등이 있는데 그 수와 같은(또는 그 배수인) winding을 갖는 구조로 되어 있다. 이들 중 3-phase BLDC Motor가 가장 폭넓게 범용적으로 사용되고 있다. 여기서는 이 3-phase BLDC Motor에 대하여 구체적으로 고찰하고자 한다.
BLDC Motor는 일반적인 Brush DC Motor의 구동 원리는 동일하나 구조적으로 반대인 특징 (그림 2.1.1과 그림 2.2.2 참조)이 있다. 즉, 3상 BLDC Motor의 구조는 그림2.2.3과 같이 고정자가 전기자권선으로 구성되어 있고, 회전자가 영구자석으로 되어 있어 구조적으로는 영구자석형 동기모터(Permanent Magnet Synchronous Motor: PMSM)와 유사하다. 하지만 PMSM은 역기전력이 정현파이나 BLDCM은 사다리꼴파인 것과, 고정자의 권선배치와 영구자석의 형태가 다르다는 점에서 차이가 난다. Brush DC Motor의 정류(commutation)를 정류자와 브러시에 의하여 구조적으로 이루 어 지는것에 반하여, BLDC Motor는 전기자권선이 고정되어 있으므로 이것을 전자적인 회로에 의하여 Rotor의 위치에 동기하여 이루어지게 된다.
(2) BLDC Motor의 구동해석
그림 2.2.1 과 같이 각 상에 1turn 씩 감겨있는 BLDC 의 한 상(U phase)만을 고려하면 그 권선이 분포된 영역의 면적(Su)는
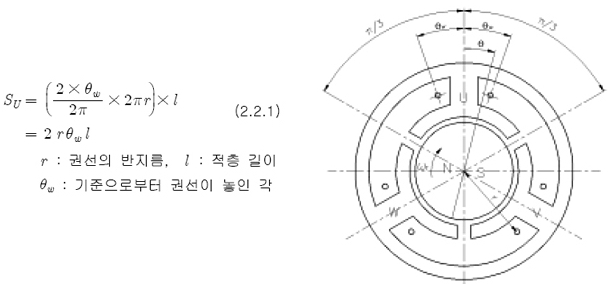
여기서 코아를 통하여 -π/3?θ?π/3 구간의 모든 Flux가 권선면 안으로 들어간다고 가정하면, U상에 놓인 N극과 S극의 면적은
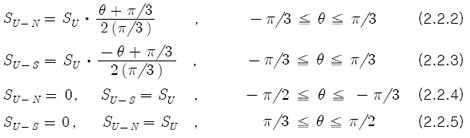
이므로 모든 곳에서 Magnetic Flux Density(B1)가 같다고 가정하면 U상에 가해지는 Flux(Φu)는
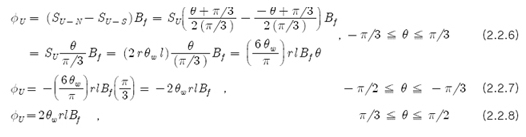
이다. 따라서, 유기되는 기전력(Φu)은
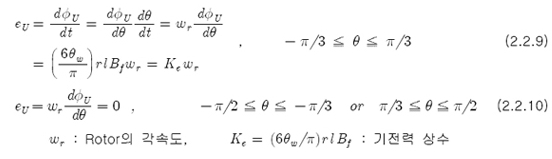
이고, 각 상에 권선된 Turn 수가 Z이고, 직렬회로수가 a(ex, 3slot → a=1, 6slot → a=2)이면 다음과 같다.
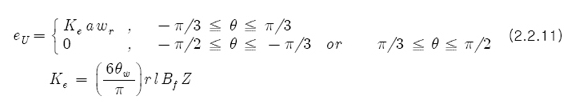
이 Flux(Φu)와 기전력(Φu)을 그래프로 나타내면 다음과 같다.
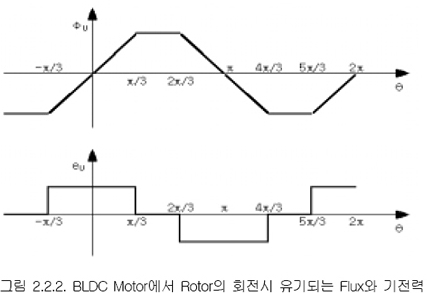
여기서 기전력이 Zero인 부분(π/3?θ?2π/3, 4π/3?θ?5π/3)의 Flux는 다른 여러 요인에 의하여 Flux가 일정한 값을 갖지 못하고 근사적으로 θ에 대한 2차 함수의 형태가 된다.
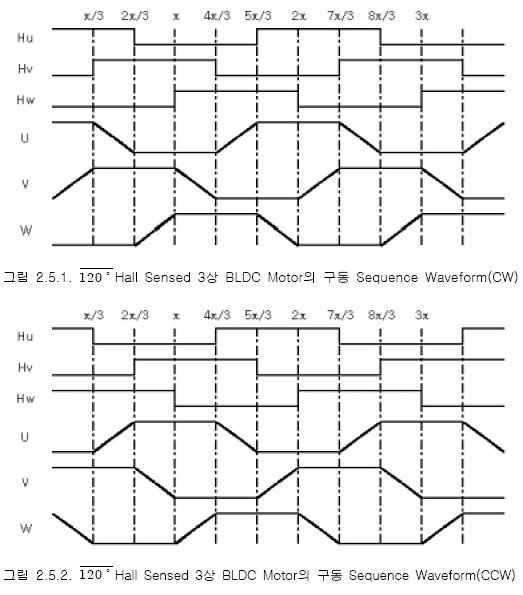
따라서 역기전력은 직선적으로 증가 또는 감소하는 형태가 되어 사다리꼴 모양으로 나타나게 된다. 그리고 다른 상(v,w상)들은 각각 120˚ 씩 뒤쳐져서 나타나게 되므로 종합하여 나타내면
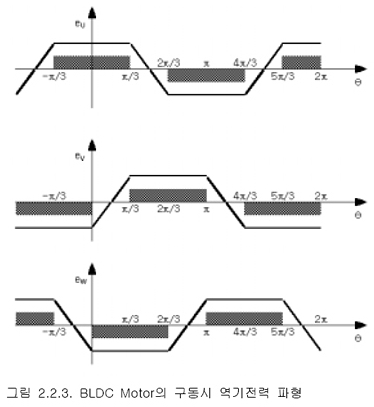
와 같다. 그림 2.2.3.에서 음영부분은 구동 전원 인가파형으로 Rotor의 위치에 따라 위 그림과 같이 각 상에 전원을 인가하도록 Switching 회로가 구성되어져야 한다.
또한, 권선방식이나 착자의 형태에 따라 연기전력은 완전한 사다리꼴의 형태를 갖추지 못한다. 이것은 증가감소구간의 비선형성을 해석하는 방법(Hague의 해석방법)과 평탄구간의 폭이 줄어드는 효과가 있는데 먼저 Hague의 해석방법은 역기전력의 평탄한 구간을 나타내면

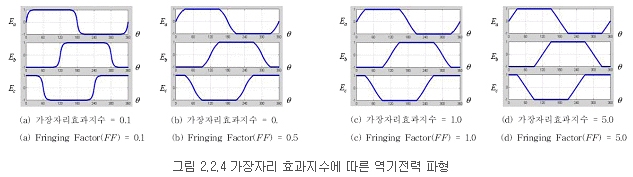
이 된다. FF의 값에 따른 파형의 변화 그래프가 그림 2.2.4와 같다.
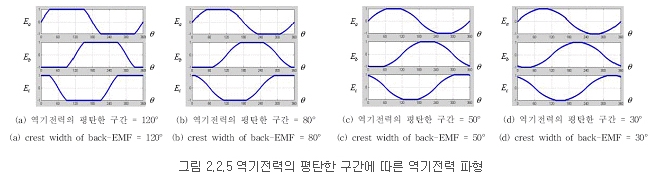
두 번째로 평탄구간의 폭이 줄어듦에 따라 역기전력은 점차 Sinusoidal 형태를 이루게 된다. 이것의 그래프는 그림 2.2.5와 같다.
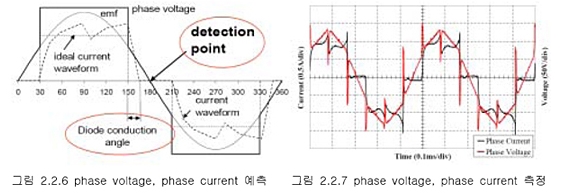
특별히 Sinusoidal Back-EMF인 경우의 상전압과 상전류의 예측파형과 실제 측정된 파형을 나타내면 그림 2.2.6과 그림 2.2.7이 된다.
(3) Motor 동작 Sequence
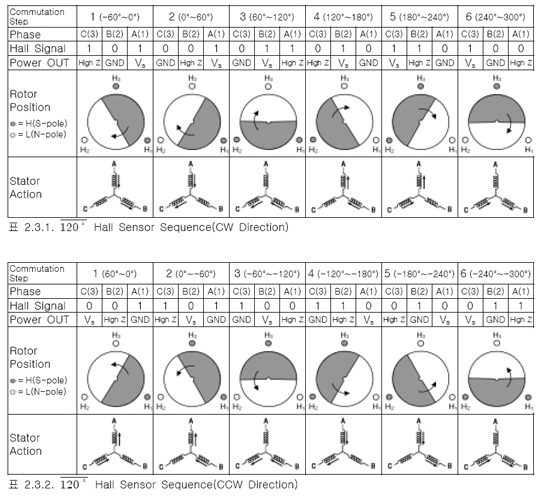
(4) Hall Sensor의 위치선정
- 표 2.3.1과 표2.3.2에서 확인 할 수 있듯이 Hall Sensor는 그 상의 권선과 CW 방향으로 120˝ 의 위치에 있어야 함을 알 수 있다.
- 여기서 Rotor의 극수가 2배가 되는 경우를 고려하면 그 각은 절반(45˚)이 됨을 알 수있다. 즉, 권선과 Hall Sensor의 각δbase는 δbase=120˚/(Pole/2)=240˚/Pole 이 된다.
- Rotor의 극수가 많아지면 그에 따라 동일한 Hall 신호를 나타낼 수 있는 대칭각이 생긴다. 예를들어 4극의 경우는 δ 가 45˚ 이지만 각에 90˚ 를 더한 각의 위치에서도 동일한 신호를 내게 된다. 즉, Rotor 에 의한 대칭각 δRsym은 δRsym = 360˚ / (Pole/2) = 720˚ / Pole 이 된다.
- Stator의 slot 수는 상수의 배수로 늘어날 경우 동일한 상의 위치에 대하여 동일한 신호를 내게 된다. 즉, Stator slot 수에 따른 대칭각 δRsym은 δRsym = 360˚ / (slot/phase) = 360˚ · phase/slot 이 된다.
그런데 slot/phase 는 rotor의 극수의 배수(m · slot/phase = pole/2, m은 자연수)로 나타나므로 δRsym = 360˚ · m · 2/pole = m · 720˚/pole = m · δRsym 이 되어 Rotor 의 대칭성에 의하여 나타나는 중복성과 같은 위치에서 나타난다. 그러므로 이것은 고려하지 않아도 된다.
- 따라서 각상의 권선과 그 상의 Hall Sensor 의 각(δ) 은

(5) 120˚ Hall Sensed 3상 BLDC Motor의 구동 Sequence Waveform